Question

Find the length of BC.B664°Note: Use either the pi button on your calculator or 3.14 for pi. Round to the nearest tenth.

Answer 1

To answer this question, we need to remember that we are going to have a fraction of the circumference (2*pi*r) of that circle. To find the length of the arc BC, we have that the radius is equal to 6 (units) and the central angle is equal to 64. Then, we have:

`\frac{\text{arc}_-\text{length}}{2\pi r}=(central_-angle)/(360)`

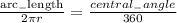
We will use for pi = 3.14, central angle = 64, r = 6:

`arc_-length=(64)/(360)\cdot2\cdot3.14\cdot6\Rightarrow A_(length)=6.69866666667`

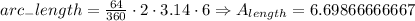
If we round the result to the nearest tenth, we have that the length of BC is equal to 6.7 (units).