Let us revise some rules of exponents
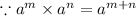
If we have two equal bases multiply by each other then we add their exponent like the rule above
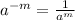
If a base has a negative exponent, then we can change the exponent to positive by reciprocal the base as the rule above
Let us use these 2 rules to solve the question
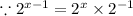
We used the first rule above
Now we can change the exponent -1 by 1 using the 2nd rule above
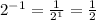
Then the answer will be
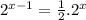
Answer a.