Question

A city has a population of 400,000 people. Suppose that each year the population grows by 7%. What will the population be after 12 years? Round your answer to the nearest whole number

Answer 1

Given:

The initial population is P(0) = 400,000.

The rate of growth is r = 7% = 0.07.

The elapsed number of years is t = 12 years.

The objective is to find the final population.

Step-by-step explanation:

The general formula to find the population is,

`P=P_0e^(rt)\text{ . . . . . .(1)}`

On plugging the given values in equation (1),

`P=400,000* e^(0.07*12)`

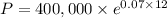
On further solving the above equation,

`\begin{gathered} P=400,000* e^(0.84) \\ =926546.79071\ldots\ldots \\ \approx926547 \end{gathered}`

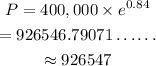
Hence, the final population after 12 years is 926547.