Question

A company sells three types of gift baskets. The basic basket has two movie passes and one package of microwave popcom. and costs $15.50. The medium basket has two movie passes, two packages of microwave popcom. and one DVD, and costs $37. The super basket has four movic passes, three packages of microwave popcom, and uwo DVDs, and costs $7.50. a. Write an augmented matrix to represent the Situation b. Use a graphing Calculator to find the cost of each Cinema

Answer 1

We know that

• The basic basket has two movie passes and one package of microwave popcorn and costs $15.50.

,

• The medium basket has two movie passes, two packages of microwave popcorn, and one DVD, and costs $37.

,

• The super basket has four movie passes, three packages of microwave popcorn, and two DVDs, and costs $7.50.

First of all, a matrix represents a system of linear equations. So, let's call x movies, y popcorn, and z DVDs. The equations would be

`\begin{gathered} 2x+1y=15.50 \\ 2x+2y+1z=37 \\ 4x+3y+2z=72.50 \end{gathered}`

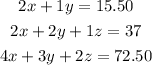
Now, arranged as a matrix would be

`\begin{bmatrix}{2} & 1{} & {0} \\ {2} & {2} & {1} \\ {4} & {3} & {2}\end{bmatrix}`

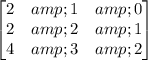
This matrix above is for coefficients.

`\begin{bmatrix}{15.50} & {} & \\ {37} & {} & {} \\ {72.50} & & {}\end{bmatrix}`

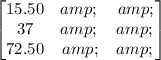
This matrix is formed by independent terms.

So, the whole matrix system would be

`\begin{bmatrix}{2} & {1} & {0} \\ {2} & {2} & {1} \\ {4} & {3} & {2}\end{bmatrix}=\begin{bmatrix}{15.50} & & \\ {37} & {} & {} \\ {72.50} & {} & \end{bmatrix}`

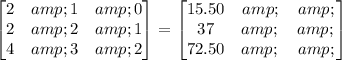
On the other hand, using a calculator, we find the value for each variable.

`\begin{gathered} x=7 \\ y=(3)/(2)=1.5 \\ z=20 \end{gathered}`

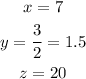
That is, each movie costs $7, each popcorn costs $1.5, and each DVD costs $20.