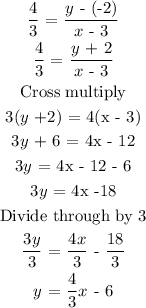Question

Line A is perpendicular to line b line a passage through the points (4,6) and (0,9) line b passes through the point (3,-2) find the equation of line b in slope intercept form

Answer 1

Step 1: Concept

First, you will need to find the equation of line A

Find the equation of a line A passing through (4,6) and (0,9).

Step 2: Find the equation of a line using two-points form

The two-points formula below will help you to find the equation of line A.

`\frac{y-y_1}{x-x_1\text{ }}\text{ = }(y_2-y_1)/(x_2-x_1)`
`\begin{gathered} x_1\text{ = 4} \\ y_1\text{ = 6} \\ x_2\text{ = 0} \\ y_2\text{ = 9} \end{gathered}`

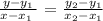
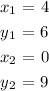
Step 3: Substitute the values in the two-point equation

Equation of a line A

`\begin{gathered} \frac{y\text{ - 6}}{x\text{ - 4}}\text{ = }\frac{9\text{ - 6}}{0\text{ - }4} \\ \frac{y\text{ - 6}}{x\text{ - 4}}\text{ = }(3)/(-4) \\ \text{Cross multiply} \\ -4(y\text{ - 6) = 3(x - 4)} \\ -4y\text{ + 24 = 3x - 12} \\ -4y\text{ = 3x -24 - 12} \\ -4y\text{ = 3x - 36} \\ \text{Divide through by -4} \\ (-4y)/(-4)\text{ = }(3x)/(-4)\text{ + }(-36)/(-4) \\ y\text{ = }(-3)/(4)x\text{ + 9} \end{gathered}`

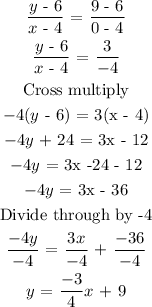
From slope intercept formula, y = mx + c, the slope of line A m1 = -3/4

Step 4:

To find the equation of line B, use the condition of perpendicularity.

Two lines are perpendicular if the product of their slopes is -1.

`\begin{gathered} \text{slope of line A m}_1\text{ = }(-3)/(4) \\ \text{Slope of line B m}_2\text{ = ?} \\ m_1m_2\text{ = -1} \\ (-3)/(4)m_2\text{ = -1} \\ \text{Cross multiply} \\ -3m_2\text{ = -1 x 4} \\ -3m_2\text{ = -4} \\ m_2\text{ = }(-4)/(-3) \\ m_2\text{ = }(4)/(3) \end{gathered}`

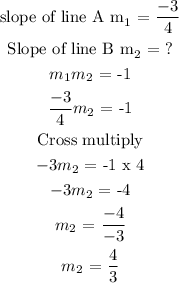
Step 5: Use slope and a point form to find the equation of line B

The slope and one-point form equation of a line is given below.

`\begin{gathered} \text{m = }(y-y_1)/(x-x_1) \\ \end{gathered}`

Since line B pass through (3,-2)

`\begin{gathered} x_1=3_{} \\ y_1\text{ = -2} \\ m_2\text{ = }(4)/(3) \end{gathered}`

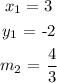
Therefore, the equation of line B is

`\begin{gathered} (4)/(3)\text{ = }\frac{y\text{ - (-2)}}{x\text{ - 3}} \\ (4)/(3)\text{ = }\frac{y\text{ + 2}}{x\text{ - 3}} \\ \text{Cross multiply} \\ 3(y\text{ +2) = 4(x - 3)} \\ 3y\text{ + 6 = 4x - 12} \\ 3y\text{ = 4x - 12 - 6} \\ 3y\text{ = 4x -18} \\ \text{Divide through by 3} \\ (3y)/(3)\text{ = }(4x)/(3)\text{ - }(18)/(3) \\ y\text{ = }(4)/(3)x\text{ - 6} \end{gathered}`