Put the following equation in the form (x+a)^2=b2x^2 + 9x = x - 368

Question

asked Oct 27, 2023 109k views

1 Answer

Shaun Xu · Answer 1 · 2023-10-31T13:36:32+0000

we are given the following equation:

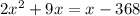
we are asked to put this equation in the form:

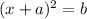
first, let's subtract x on both sides:

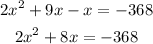
$\begin{gathered} 2x^2+9x-x=-368 \\ 2x^2+8x=-368 \end{gathered}$

Now we add 368 on both sides:

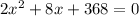
Now we will divide by "2" both sides of the equation:

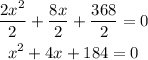
$\begin{gathered} (2x^2)/(2)+(8x)/(2)+(368)/(2)=0 \\ x^2+4x+184=0 \end{gathered}$

Now we will separate 184 as 180 + 4, like this:

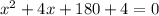
Now we will factor the expression as a perfect square trinomial, like this:

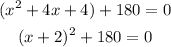
$\begin{gathered} (x^2+4x+4)+180=0 \\ (x+2)^2+180=0 \end{gathered}$

Now we will subtract 180 on both sides:

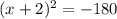
And thus we have obtained the desired form for the expression.