We have that the point V is on the line segment UW. This represents a situation similar to this:
In this case, we get that:
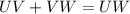
Which means that:
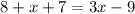
Clearing out the variable x, we obtain that:
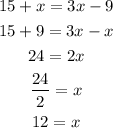
Now, we just have to replace the value of x on the equation of UW, and we obtain:
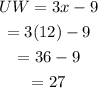
This means that the value of UW is 27.