Question

A rollercoaster has a mass of 140 kilograms and starts rolling from rest down a hill that is 13.8 meters high. The rollercoaster rolls to the bottom of the hill and then up a smaller hill that is 4.9 meters high. What is the velocity of the roller coaster as it moves over the second hill? Disregard air resistance and friction. Round your answer to the nearest tenth of a meter per second.

Answer 1

13.2 m/s

Step-by-step explanation

Step 1

Diagram

the law of conservation of energy states that the total energy of an isolated system remains constant; it is said to be conserved over time. so, if we ignore the friction, we can se apply this to set an equation

`Energy\text{ at A= Energy at B}`

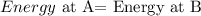
a) At a , the rollercoaster has

potential gravitational energy ( due to the heigth), as it start from the rest the velocity is zero,s o the kinetick energy is zero

b) at B, the rollercoster has

potential gravitational energy ( due to the heigth) and kinetick energy ( due to its mass ena velocity)

hence

`\begin{gathered} Energy\text{ at A= Energy at B} \\ 0+mgh_1=(1)/(2)mv^2+mgh_2 \end{gathered}`

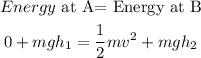
Step 2

let

`\begin{gathered} mass\text{ =}140\text{ kg} \\ h_1=13.8 \\ h_2=4.9 \\ \end{gathered}`

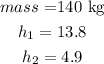
replace and solve for v

`\begin{gathered} \begin{equation*} mgh_1=(1)/(2)mv^2+mgh_2 \end{equation*} \\ m\left(gh_1\right)=m\left((1)/(2)v^2+gh_2\right? \\ (gh_1)=(1)/(2)v^2+gh_2 \\ swubtract\text{ gh}_2\text{ in both sides} \\ (gh_1)-gh_2=(1)/(2)v^2 \\ g\lparen h_1-h_2)=(1)/(2)v^2 \\ \begin{equation*} \end{equation*} \\ \\ \end{gathered}`

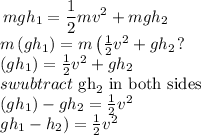
so

therefore, the answer is

13.2 m/s

I hope this helps you