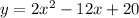Answer:
Step-by-step explanation:
The vertex form of the equation of a parabola is given as:

Given that the vertex (h,k)=(3,2)
We have:
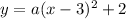
Since it goes through the point (1,14):
x=1, y=14
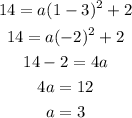
The equation of the parabola is:
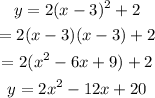
The equation of the parabola is: