ANSWER
7.95 m/s
Step-by-step explanation
The least initial velocity is the one for which when the object reaches the height of the platform its velocity is zero. From the velocity equation we have,
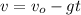
If v = 0,
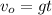
To find the velocity we have to find the time. From the displacement equation,

Replace v0 by the expression above,

We know that the height of the platform is 3.2m. Solving this equation for t,
![t=\sqrt[]{(2y)/(g)}=\sqrt[]{(2\cdot3.2m)/(9.81m/s^2)}\approx0.81s](https://img.qammunity.org/2023/formulas/physics/high-school/v5mypn5jff829lg8vl28p2onjoi2dgtnmi.png)
If the object is in the air for 0.81 seconds before reaching the platform, its initial velocity is,
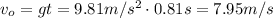
The least initial velocity needed from ground level for the object to reach the platform is 7.95 m/s