Given:
a.) There are 70.8 m of fencing around a rectangular field.
- Perimeter = 70.8 m
b.) The length of the field is 20.4 m
Since it's been mentioned that the fencing around a rectangular field is 70.8 m. We can say that the perimeter of the field must be 70.8 m.
Given the measure of its length, to be able to get the measure of its width, we will be using the rectangle's perimeter formula:
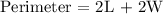
We get,
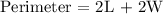
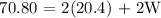
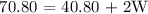
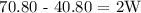
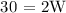
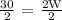
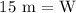
Therefore, the measure of the Width is 15 m.