Solution
Given that;
There are 6 red marbles and 10 white marbles
Total marbles is
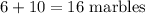
To find the probability of randomly choosing a marble, the formula is
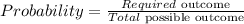
Let the probability of randomly choosing a white marble be represented by P(W)
Where the
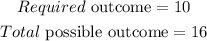
The probability of randomly choosing a white marble, P(W) is
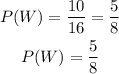
Hence, the probability of randomly choosing a white marble, P(W) is 5/8