Question

How do i find what g(x) and f(x) are equal to

Answer 1

Step-by-step explanation

When multiplying expressions with multiple terms we must use the distributive property of the multiplication:

`(a+b)(c+d)=a(c+d)+b(c+d)=ac+ad+bc+bd`

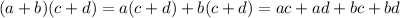
It is also important to remember that when we multiply polynomial terms constants and powers of x are multiplied separately:

`ax^n\cdot bx^m=a\cdot b\cdot x^n\cdot x^m=abx^(n+m)`

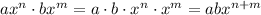
Now we can proceed. We apply the distributive property to the product between f(x) and g(x):

`\begin{gathered} f(x)\cdot g(x)=(x^2+3x-4)(x+5)=x^2(x+5)+3x(x+5)-4(x+5) \\ x^2(x+5)+3x(x+5)-4(x+5)=x^2\cdot x+x^2\cdot5+3x\cdot x+3x\cdot5-4\cdot x-4\cdot5 \end{gathered}`

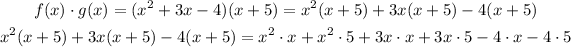
Now we continue multiplying the terms following what I stated above:

`x^2\cdot x+x^2\cdot5+3x\cdot x+3x\cdot5-4\cdot x-4\cdot5=x^3+5x^2+3x^2+15x-4x-20`

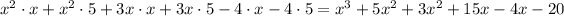
Now we have to add like terms i.e. terms with the same power of x. In order to do this we have to use the distributive property but in reverse:

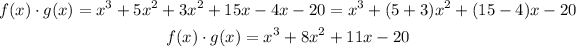
`\begin{gathered} f(x)\cdot g(x)=x^3+5x^2+3x^2+15x-4x-20=x^3+(5+3)x^2+(15-4)x-20 \\ f(x)\cdot g(x)=x^3+8x^2+11x-20 \end{gathered}`Answer

Then the answer is the third option.