Question

I need help with this question for part a and b

Answer 1

Answer: 30.2% EZ

Explanation:

Answer 2

Given

Mean life = 400 days

standard deviation = 40 days

The streetlight lifetimes are normally distributed

a) Last longer than 600 days

Convert the value to Z-score using the formula:

`\begin{gathered} z\text{ = }\frac{x\text{ -}\mu}{\sigma} \\ \text{Where }\mu\text{ is the mean life} \\ \text{and }\sigma\text{ is the standard deviation} \end{gathered}`

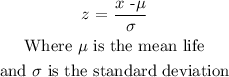
Hence:

`\begin{gathered} z\text{ = }\frac{600\text{ - 400}}{40} \\ =\text{ }(200)/(40) \\ =\text{ 5} \end{gathered}`

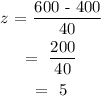
Using the probability from z-score table, we can find the percentage of the lamps that would last longer than 600 days.

Hence:

`P(x>z)=0`

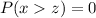
Answer: No streetlight would last longer than 600 days

b) Last between 420 and 500 days

The z-scores for the given days:

`\begin{gathered} z_(420)\text{ = }\frac{420\text{ - 400}}{40} \\ =\text{ 0.5} \end{gathered}`
`\begin{gathered} z_(500)\text{ = }\frac{500\text{ -400}}{40} \\ =\text{ }(100)/(40) \\ =\text{ 2.5} \end{gathered}`

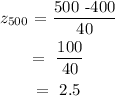
Using the probability from z-score table, the percentage of streetlights that would last between 420 and 500 days:

[tex]P(0.5\text{ Answer: 30.2%

The sketch of the solution: