Question

Making a Cylinder: Make an 8 1/2 by 11 inch piece of notebook paper into a cylinder as shown. Use the diagrams to help with the following questions.

Answer 1

`\begin{gathered} a)1.353\text{ inches = radius max} \\ b)\text{Area}_s=105(in^2) \\ c)\text{Area}=93.5(in^2) \end{gathered}`

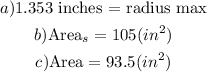
Step-by-step explanation

Step 1

a)

Let

`\text{length}=\text{ 11 inches}`

the circle of the base will a arc of

`\text{perimeter}=\text{ 2 }\pi r`

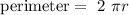
also, we know that perimeter of the circle equals the width of the paper, so

`\begin{gathered} 8(1)/(2)=2\text{ }\pi\text{ r} \\ 8.5=2\pi r \\ \text{divide both sides by 2}\pi \\ (8.5)/(2\pi)=(2\pi r)/(2\pi) \\ 1.3528\text{ inches = radius} \\ \text{rounded} \\ r=1.353 \end{gathered}`

hence

the largest possible radius is 1.35 inches

Step 2

let

`\begin{gathered} \text{radius}=1.353\text{ in} \\ \text{height}=11\text{ in} \end{gathered}`

the total surface area of a cylinder is given by

`\text{Area}_s=2\pi r(r+h)`

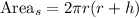
then, replace

`\begin{gathered} \text{Area}_s=2\pi r(r+h) \\ \text{Area}_s=2\pi(1.353\text{ in)(1.353 in+11 in)} \\ \text{Area}_s=2\pi(1.353\text{ in)(12.353 in)} \\ \text{Area}_s=105.01470(in^2) \\ \text{rounded} \\ \text{Area}_s=105(in^2) \end{gathered}`

Step 3

the area of the original paper

it is a rectangle, the area of a rectangle is given by:

`\text{Area}=\text{length }\cdot width`

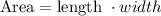
Let

length= 11 inches

width=8.5 inches

replace

`\begin{gathered} \text{Area}=\text{length }\cdot width \\ \text{Area}=11\text{ in }\cdot8.5\text{ in} \\ \text{Area}=93.5(in^2) \end{gathered}`

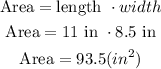
I hope this helps you