Given that x varies directly with y, we have that:
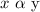
Now, we replace the sign of proportionality with the contant k, as follows:
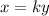
Now, since we have a pair of values already given for x and y, we directly substitute those values into the equation above in order to obtain the value of the constant, as shown below:
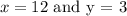
Thus:
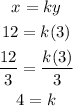
Thus, we have the value of the constant k to be equal to 4.
Now, we have the equation to be:
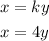
Finally, we make y the subject, as follows:
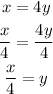
Therefore:
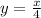
or:
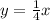
The value that goes into the numerator in the i