Question

Solve the equation by completing the square. 4x^2-30x=12+10x

Answer 1

We are given the following quadratic equation

`4x^2-30x=12+10x`

Let us solve this equation by completing the square method.

First of all, simplify the equation a bit

`\begin{gathered} 4x^2-30x=12+10x \\ 4x^2-30x-10x-12=0 \\ 4x^2-40x-12=0 \end{gathered}`

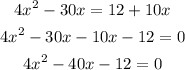
Step 1:

Divide the equation by 4 (to make the coefficient of the square term 1)

`\begin{gathered} (4x^2-40x-12)/(4)=(0)/(4) \\ x^2-10x-3=0 \end{gathered}`

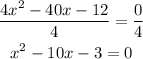
Step 2:

Move the constant term to the right side

`x^2-10x=3`

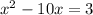
Step 3:

Add half of the square of the coefficient of x-term to both sides of the equation

The coefficient of x-term is -10

`x^2-10x+((-10)/(2))^2=3+((-10)/(2))^2`

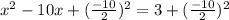
Simplify

`\begin{gathered} x^2-10x+(-5)^2=3+(-5)^2 \\ x^2-10x+25^{}=3+25^{} \\ x^2-10x+25^{}=28 \end{gathered}`

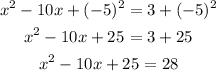
Step 4:

Apply the difference of squares formula on the left side of the equation

`(a-b)^2=a^2-2ab+b^2`

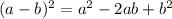
In this case, a = x and b = 5

`(x-5)^2=28`

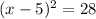
Step 5:

Now we can solve the equation for x.

Take square root on both sides of the equation

`\begin{gathered} \sqrt[]{\mleft(x-5\mright)^2}=\sqrt[]{28} \\ (x-5)=\pm\sqrt[]{28} \\ (x-5)=\pm2\sqrt[]{7} \end{gathered}`

Step 6:

Find the two possible solutions of x

`\begin{gathered} x-5=2\sqrt[]{7}\quad and\quad x-5=-2\sqrt[]{7} \\ x=5+2\sqrt[]{7}\quad and\quad x=5-2\sqrt[]{7} \\ x=5+5.29\quad and\quad x=5-5.29 \\ x=10.29\quad and\quad x=-0.29 \end{gathered}`

Therefore, the solution of the given quadratic equation is

`\begin{gathered} x=(5+2\sqrt[]{7},5-2\sqrt[]{7}) \\ x=(10.29,-0.29) \end{gathered}`