a) Value of invest when compounded annually= $72878.67
b) Value of invest when compounded semi-annually is $73420.12
c) Value of invest when compounded monthly is $73896.35
Step-by-step explanation
a)Annually
Given:
Principal(p)= 49600
rate (r) = 8% = 0.08
time(t) =5
Since it is compounded anually, n=1
Using the formula;
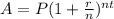
Substitute the value and evaluate.
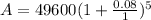
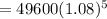
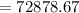
Therefore, the value of the investment when compounded annually is $72878.67
b) Semi-annually
In this case, the we are going to substitute all our initial values except for n.
In the case of semi annually, n= 2
That is;
Principal(p)= 49600
rate (r) = 8% = 0.08
time(t) =5
n=2
Substitute into the formula and evaluate.
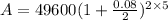
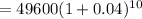
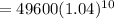
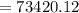
Therefore, the value of the investment when compounded semi-annually is $73420.12
c)monthly
In this case n= 12 and all other values remains the same.
That is;
Principal(p)= 49600
rate (r) = 8% = 0.08
time(t) =5
n=12
Substitute the values into the formula and evaluate.
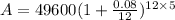
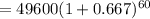
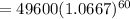
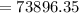
Therefore, the value of the investment when compounded monthly is $73896.35