Question

the basketball coach is selecting from nine starters who will be the first three batters how many different batters lineups can the coach consider for the first three up?

Answer 1

We know that

• The total is nine starters.

,

• The coach wants to choose three.

Given that the player cannot include repetition, we solve this problem as a combination because the order does not matter.

`C^r_n=(n!)/(r!(n-r)!)`

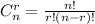
Where n = 9, and r = 3. Let's replace these values.

`C^3_9=(9!)/(3!(9-3)!)=(9!)/(3!\cdot6!)=(9\cdot8\cdot7\cdot6!)/(3\cdot2\cdot1\cdot6!)=(504)/(6)=84`

Hence, there are 84 different ways to choose the first three.