Answer:
The value of U is 4.
The value of W is -6.
The value of V is 5.
The value of Z is 1.
The value of x is 3
The value of y is 2.
Explanation:
Let's equal both expressions:
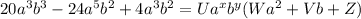
Now we factorize the expression on the left-side of the equality, finding the common terms.
Between 20, 24, 4.
Divisors of 20 = {1,2,4,5,10,20}
Divisors of 24 = {1,2,3,4,6,8,12,24}
Divisors of 4 = {1,2,4}
Greatest common divisor: 4, which is the common term.
Between a^3,a^5,a^3
The one with the lowest exponent, which is a^3
Between b^3,b^2,b^2
Lowest exponent is b^2
Common term: 4*a³*b²
So the expression can be rewritten as:
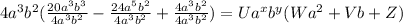
Now we solve the divisions:
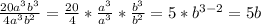
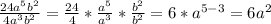
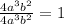
Replacing:
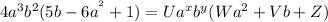
Just a small adjustment for formatting
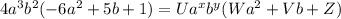
Now, comparing the left side of the equality with the right side.
U = 4, x = 3, y = 2, W = -6, V = 5, Z = 1.
The value of U is 4.
The value of W is -6.
The value of V is 5.
The value of Z is 1.
The value of x is 3
The value of y is 2.