The 68-95-99.7 rule states that:
• 68% of the data is expected to be within one standard deviation from the mean.
• 95% of the data is expected to be within two standard deviations from the mean.
• 99.7% of the data is expected to be within three standard deviations from the mean.
Then, when the mean is $19,000 and the standard deviation is $500, we can estimate how many standard deviations we are from the mean for the values $17500 and $19000 calculating the z-score:
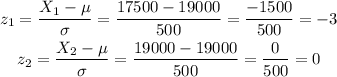
Then, we have three standard deviations to the left and no standard deviation from the mean for the right boundary.
We can picture this in the normal distribution curve as:
This is half the amount of data that if we have 3 standard deviations to each side of the mean, so we can expect to have 99.7% / 2 = 49.85% of the data within these limits.
Answer: 49.85%