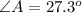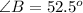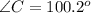Question

Use Law of Sines and Cosines to find the missing measurements. Round all answers to the nearest tenth. Please show work

Answer 1

Given:

The boat heads west for 3700 m. The other two sides lie the north for the first side, and their lengths are 1700m and 3000m.

The diagram for this model is

Using cosine law to find the angle of C.

`c=\sqrt[]{a^2+b^2-2ab\cos C}`

Taking square on both sides, we get

`c^2=a^2+b^2-2ab\cos C`

`\cos C=(a^2+b^2-c^2)/(2ab)`

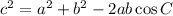
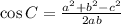
Substitute a=1700, b=3000 and c=3700, we get

`\cos C=(1700^2+3000^2-3700^2)/(2*1700*3000)`

`\cos C=(-1800000)/(10200000)=-0.17647`
`\angle C=\cos ^(-1)(-0.17647)`

`\angle C=100.164^o`
`\angle C=100.2^o`

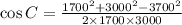
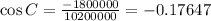
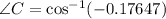
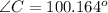
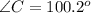
Hence the measure of angle C is 100.2 degrees.

Using sine law,

`(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`

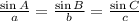
Substitute a=1700, b=3000 and c=3700, and angle C=100.2 degrees, we get

`(\sin A)/(1700)=(\sin B)/(3000)=(\sin 100.2^o)/(3700)`
`U\text{se }\sin 100.2^o=0.9842.`

`(\sin A)/(1700)=(\sin B)/(3000)=\frac{0.9842^{}}{3700}`

`(\sin A)/(1700)=(\sin B)/(3000)=0.00027`

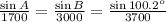
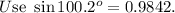
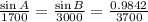
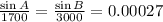
Consider

`(\sin A)/(1700)=0.00027`

`\sin A=0.00027*1700`

`\sin A=0.459`

`\angle A=\sin ^(-1)(0.459)`
`\angle A=27.322`

`\angle A=27.3^o`

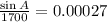
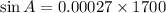
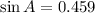
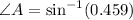
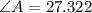
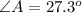
Hence the angle of A is 27.3 degrees.

Using triangle sum property, we get

`\angle A+\angle B+\angle C=180^o`

`\angle B=180^o-\angle A-\angle C`
`\text{ Substitute }\angle A=27.3^o\text{ and }\angle C=100.2^o\text{, we get}`

`\angle B=180^o-27.3^o-100.2^o`

`\angle B=52.5^o`

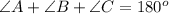
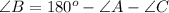
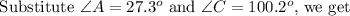
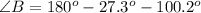
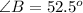
Hence the angle of B is 52.5 degrees.

Results:

`\angle A=27.3^o`
`\angle B=52.5^o`
`\angle C=100.2^o`