Given:
The length of the arc is (1/12) x circumference of unit circle.
The objective is to find the area of the sector.
Since it is given as a unit cirle, the radius of the circle will be 1 unit.
The circumference of the circle will be,
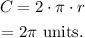
Then, the length of the arc will be,
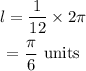
Now, the formula to find the area of the sector is,
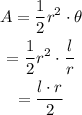
On plugging the values in the above relation,
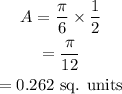
Hence, the area of the sector is 0.262 square units.