8) y= V1-5 A) Domain: x 20 Range: y 2-5 B) Domain: x > 0 Range: y'z 5 C) Domain: {All real numbers. } Range: {All real numbers. } D) Domain: x 25 Range: y 20

Question

asked Nov 16, 2023 214k views

1 Answer

Remosu · Answer 1 · 2023-11-22T20:37:24+0000

$y=\sqrt[]{x}-5$

Domain:

we know that a root cannot have negative values inside so

$\begin{gathered} \sqrt[]{x}\ge0 \\ x\ge0^2^{} \\ x\ge0 \end{gathered}$

the domain is X >= 0

Range:

we solve the equation for y

$\begin{gathered} y=\sqrt[]{x}-5 \\ y+5=\sqrt[]{x} \\ (y+5)^2=x \end{gathered}$

and we replace the condition that x must be greater than or equal to 0

so

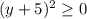
$(y+5)^2\ge0$

now solve y

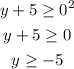
$\begin{gathered} y+5\ge0^2 \\ y+5\ge0 \\ y\ge-5 \end{gathered}$

so the range is Y >= -5

then the right option is A