Question

What is the present value of an investment that will be worth $7000 at the end of five years? Assume an APR of 6% compounded monthly. (Round your answer to the nearest cent.)

Answer 1

The Solution:

Let the present value of the investment be represented with P.

We shall use the formula below:

`\begin{gathered} A=P(1+(r)/(100\alpha))^(n\alpha) \\ \text{Where} \\ A=\text{amount (after 5years)}=\text{ \$7000} \\ r=rate\text{ (in \%)=6 \%} \\ n=\text{ number of years =5 years} \\ \alpha=\text{ number of periods per annum =12} \\ P=\text{ Principal = initial investment=?} \end{gathered}`

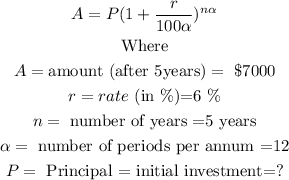
Substituting these values in the formula above, we get

`\begin{gathered} 7000=P(1+(6)/(100*12))^((5*12)) \\ \\ 7000=P(1+(6)/(1200))^(60) \end{gathered}`

So,

`\begin{gathered} 7000=P(1+0.005)^(60) \\ \\ 7000=P(1.005)^(60) \\ \text{Dividing both sides by 1.005}^(60),\text{ we get} \\ P=(7000)/(1.005^(60))=(7000)/(1.348850153)=5189.605\approx\text{ \$5189.61 (518961cent)} \end{gathered}`

Thus, the present value of the investment that will yield $7000 at the end of 5 years is $5189.61 (or 518961 cents )

Therefore, the correct answer is $5189.61 (or 518961 cents )