Question

Large drinks cost $2.75 each and medium drinks cost $2.15 each. A restaurant sold 52 drinks yesterday and took in a total of $131.60. How many medium drinks did they sell?

Answer 1

To solve this type of question we need to form 2 equations of 2 variables and solve them to find the 2 variables

Let x is the number of the large drinks and y is the number of the medium drinks

Since the restaurant sold 52 drinks, then

`x+y=52\rightarrow(1)`

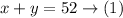
Since the cost of the large drink is $2.75 each, then

The cost of the large drinks is 2.75(x)

Since the cost of the medium drink is $2.15 each, then

The cost of the medium drinks is 2.15(y)

Since the total cost of them is $131.60, then

Add 2.75(x) and 2.15(y) and equate the sum by 131.60

`\begin{gathered} 2.75(x)+2.15(y)=131.60 \\ 2.75x+2.15y=131.60\rightarrow(2) \end{gathered}`

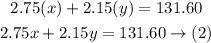
Now we have a system of equations to solve it

Multiply equation (1) by -2.75 to make x equal in values of the two equations and different in signs to eliminate it

`\begin{gathered} (-2.75)x+(-2.75)y=(-2.75)(52) \\ -2.75x-2.75y=-143\rightarrow(3) \end{gathered}`

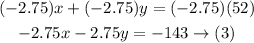
Add equations (2) and (3)

`\begin{gathered} 2.75x+2.15y+(-2.75x)+(-2.75y)=131.60+(-143) \\ (2.75x-2.75x)+(2.15y-2.75y)=131.6-143 \\ 0-0.6y=-11.4 \\ -0.6y=-11.4 \end{gathered}`

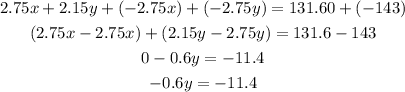
Divide both sides by -0.6

`\begin{gathered} (-0.6y)/(-0.6)=(-11.4)/(-0.6) \\ y=19 \end{gathered}`

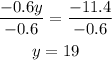
They sold 19 medium drinks yesterday