We are asked to find the degree of the following polynomial:
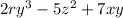
Recall that the degree of a polynomial is the sum of all number of letter factors in the term of the polynomial that contains more letter factors (this is often called the leading term of the polynomial)
In our case, we have:
1) in the first term, one factor "r", and three factors "y" therefore, a total of 4
2) in the second term, two factors "z" so a total of 2
3) in the third term, one factor "x" and one "y" ; therefore a total of 2
Then, the leading term of the polynomial is the first one , and it has a total of 4 letter factors, therefore its degree is 4 and it is as well the degree of the polynomial (since the leading term defines the degree of the entire polynomial).
Degree of the polynomial = 4.
Extra question from user:
"how can i solve (-6s)^2"
Notice that (-6 s)^2 is the product of (-6 s) times {-6 s) *that is the meaning of the square symbol", then you multiply each expression times the other. Start with the negative sign:
- * - = + (the rule that tells us negative times negative renders positive)
now the numerical part: 6 * 6 = 36
and finally the letter part: s * s = s^2
So the answer is: positive 36 s^2