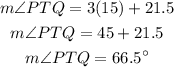Set 4 Use the figure for numbers 1 - 3. 1. M

Question

asked Dec 26, 2023 22.7k views

1 Answer

Indrid · Answer 1 · 2024-01-01T14:43:59+0000

From the given figure

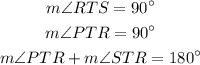
$\begin{gathered} m\angle RTS=90^(\circ) \\ m\angle PTR=90^(\circ) \\ m\angle PTR+m\angle STR=180^(\circ) \end{gathered}$

1.

Since

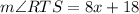
$m\angle RTS=8x+18$

Then equate 8x + 18 by 90 to find x

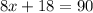
Subtract 18 from both sides

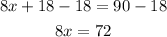
$\begin{gathered} 8x+18-18=90-18 \\ 8x=72 \end{gathered}$

Divide both sides by 8

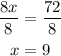
$\begin{gathered} (8x)/(8)=(72)/(8) \\ x=9 \end{gathered}$

The value of x is 9

2.

Since

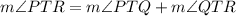
$m\angle PTR=m\angle PTQ+m\angle QTR$

Then equate the right side by 90 degrees

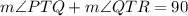
$m\angle PTQ+m\angle QTR=90$

Since

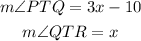
$\begin{gathered} m\angle PTQ=3x-10 \\ m\angle QTR=x \end{gathered}$

Then

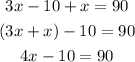
$\begin{gathered} 3x-10+x=90 \\ (3x+x)-10=90 \\ 4x-10=90 \end{gathered}$

Add 10 to both sides

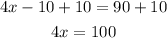
$\begin{gathered} 4x-10+10=90+10 \\ 4x=100 \end{gathered}$

Divide both sides by 4

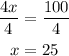
$\begin{gathered} (4x)/(4)=(100)/(4) \\ x=25 \end{gathered}$

The value of x is 25

3.

Since

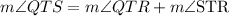
$m\angle QTS=m\angle QTR+m\angle\text{STR}$

Then

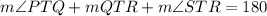
$m\angle PTQ+mQTR+m\angle STR=180$

Substitute their values

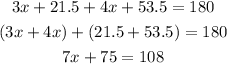
$\begin{gathered} 3x+21.5+4x+53.5=180 \\ (3x+4x)+(21.5+53.5)=180 \\ 7x+75=108 \end{gathered}$

Subtract 75 from both sides

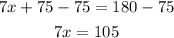
$\begin{gathered} 7x+75-75=180-75 \\ 7x=105 \end{gathered}$

Divide both sides by 7

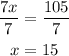
$\begin{gathered} (7x)/(7)=(105)/(7) \\ x=15 \end{gathered}$

Substitute x by 15 in the measure of
$\begin{gathered} m\angle PTQ=3(15)+21.5 \\ m\angle PTQ=45+21.5 \\ m\angle PTQ=66.5^(\circ) \end{gathered}$