Question

Write a function that fits the following criteria:1. Vertical asymptotes at 1 and 42. Zeroes at 3 and 53. Hole at (6,3)

Answer 1

To construct a function that has vertical asymptotes ar 1 and 4 we write a rational function as follows:

`g(x)=(kP(x))/((x-1)(x-4))\text{.}`

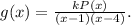
Now, for g(x) to have zeros at 3 and 5, P(x) must be as follows:

`P(x)=(x-3)(x-5)\text{.}`

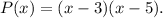
Therefore:

`g(x)=(k(x-3)(x-5))/((x-1)(x-4))\text{.}`

Finally, since the function must have a hole at (6,3) we divide and multiply by (x-6):

`g(x)=(k(x-3)(x-5)(x-6))/((x-1)(x-4)(x-6))\text{.}`

Since the hole must have y-coordinate 3, then k must be:

`k=10.`

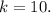
Therefore, if f(x) is the function we are looking for:

`f(x)=(10(x-3)(x-5)(x-6))/((x-1)(x-4)(x-6))\text{.}`

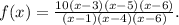
Answer: Option C.