Question

Write an equation describing the relationship of the given variables Y varies directly as x and when x=6, y=54

Answer 1

Given:

`\begin{gathered} y\alpha x \\ x=6,y=54 \end{gathered}`

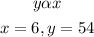
To Determine: The equation describing the relationship between y and x

Solution:

Step 1: Introduce the constant into the given variation

`\begin{gathered} y=kx \\ k=\text{constant} \end{gathered}`

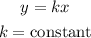
Step 2: Substitute the given values of y and x to find the constant

`\begin{gathered} y=kx,x=6,y=54 \\ k=(y)/(x) \\ k=(54)/(6) \\ k=9 \end{gathered}`

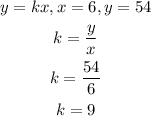
Step 3: Substitute k into the equation

`\begin{gathered} y=kx,k=9 \\ y=9x \end{gathered}`

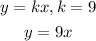
Hence, the equation describing the relationship between x and y is

y = 9x