Question

Find the volume of the composite solid to the nearest whole number.

Answer 1

To determine the volume of the given solid, we will divide it into two solids:

Solid A, which is a cobblestone, with sides 14in x 11in x 23in.

Solid B, half-cylinder with a base diameter equal to 14in and height equal to 11in.

Now, we are able to say that the volume of the given solid is:

`V=V_A+V_B`

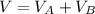
Calculating volume of Solid A:

`V_A=11*14*23=3,542\text{ in³}`

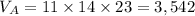
Now, using π = 3.14, we calculate the volume of Solid B:

`V_B=(1)/(2)*3.14*((14)/(2))^2_{}*11=846.23`

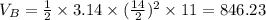
Now, we sum them:

`V=3,542+846.23=4,388.23in^(3)`

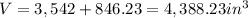
from the solution developed above, we are able to conclude that the nearest whole number which represents the volume of the given solid is: 4,388 in³