Question

Find the zeros of the function. Then sketch a graph of the function

Answer 1

We can start by doing the next substitution:

`\begin{gathered} u=x^2 \\ \rightarrow u^2=x^4 \end{gathered}`

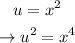
Then we have the next function:

`f(u)=u^2-18u+81`

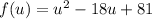
It is in the form:

`au^2+bu+c^{}`

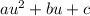
Where a=1, b=-18 and c=81.

Then we can use the quadratic formula to find the roots:

`\begin{gathered} u=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ u=\frac{-(-18)\pm\sqrt[]{(-18)^2-4(1)(81)}}{2(1)} \\ u=\frac{18\pm\sqrt[]{324-324}}{2} \\ u=\frac{18\pm\sqrt[]{0}}{2} \\ u=(18\pm0)/(2) \\ u=(18)/(2) \\ u=9 \end{gathered}`

Now, replace this value into the initial substitution:

`\begin{gathered} 9=x^2 \\ \rightarrow x=\pm\sqrt[]{9} \\ \rightarrow x=+3\text{ and x=-3} \end{gathered}`

The zeros of the function are x=3 and x=-3.

The graph is: