The formula for compound interest is:

Where A is the current amount, P is the initial amount, r is the interest rate, n is the number of times the interest is applied in a period, and t is the period. Then, in our problem,
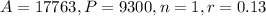
We need to solve for t, as follows:

Therefore (using numeric values),
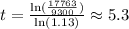
Therefore, we will reach that total amount after 5.3 years of compound interest.