From the given picture we can see 2 concentric circles, The big circle has a radius of 8 units and the small circle has a radius of 2 units
To find the area of the shaded, subtract the area of the small circle from the area of the big circle
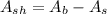
Since the area of the circle is
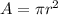
Since
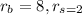
Substitute them in the rule above
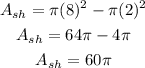
The area of the shaded is 60pi square units