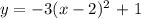Concept
Apply the equation of the vertex form below to write the quadratic function.

Next,
where
(x,y) is any point on the described parabola, (h,k) is the vertex of the parabola, and a is an unknown value that is found using the given point that is not the vertex.
The vertex is ( h, k ) = ( 2, 1 )
( x, y ) = ( 3 , -2 )
Next, substitute h, k , x and y in the equation to find the value of a.
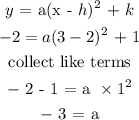
Final answer
Substitute the values of h, k and a in the original equation.