Question

Plot points between and beyond each X intercept and vertical asymptote find the value of the function at the given value of XFractions please

Answer 1

Given the function:

`f(x)=(2x^2)/(x^2+4)`

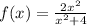
when x=-2, f(x) = ?

Substitute the value of -2 for x in the f(x) function.

`\begin{gathered} f(x)=(2x^2)/(x^2+4) \\ f(-2)=(2(-2)^2)/((-2)^2+4)=1 \end{gathered}`

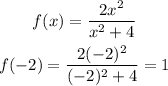
when x = -1, f(x) =?

Substitute the value of -1 for x in the f(x) function.

`\begin{gathered} f(x)=(2x^2)/(x^2+4) \\ f(-1)=(2(-1)^2)/((-1)^2+4)=(2)/(5) \end{gathered}`

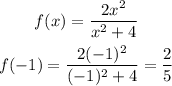
when x = 5, f(x) =?

Substitute the value of 5 for x in the f(x) function.

`\begin{gathered} f(x)=(2x^2)/(x^2+4) \\ f(5)=(2(5)^2)/((5)^2+4)=(50)/(29) \end{gathered}`

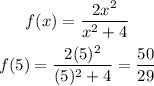
when x = 6, f(x) =?

Substitute the value of 6 for x in the f(x) function.

`\begin{gathered} f(x)=(2x^2)/(x^2+4) \\ f(6)=(2(6)^2)/((6)^2+4)=(9)/(5) \end{gathered}`

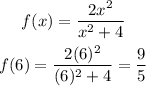
Thus, we have

`\begin{gathered} x=-2,\text{ f(}x)\text{ =}1 \\ x=-1,\text{ f(x)=}(2)/(5) \\ x=5,\text{ f(x)=}(50)/(29) \\ x=6,\text{ f(x)=}(9)/(5) \end{gathered}`

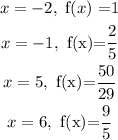
The graph of the f(x) function is as shown below: