Question

Tap A can fill a tank in 6 hours, while tap B can fill in 9 hours. In how much time will the tank be filled if both the taps are opened together?

Answer 1

3.6 hours

Step-by-step explanation:

Given the following information

Tap A fill the tank in 6hours

Tank B fill the tank in 9 hours

Let X be the time it will take the tank to be filled if both the taps are opened together

To get the value of X, we will take the sum of the reciprocal of the time taken by both tanks and equate to the reciprocal of X as shown:

`\begin{gathered} (1)/(X)=(1)/(6)+(1)/(9) \\ \frac{1}{X\text{ }}=(9+6)/(54) \\ (1)/(X)=(15)/(54) \end{gathered}`

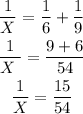
Cross multiply and find X

`\begin{gathered} 15X=54 \\ X=(54)/(15) \\ X=3.6\text{hours} \end{gathered}`

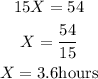
This shows that the time it will take for the tank to be filled if both the taps are opened together is 3.6 hours