Question

Steam to drive an old-fashioned steam locomotive is supplied at a constant gauge pressure of 1.55 ✕ 106 N/m2 (about 225 psi) to a piston with a 0.205 m radius.(a) By calculating PΔV, find the work done (in J) by the steam when the piston moves 0.805 m. Note that this is the net work output, since gauge pressure is used.

Answer 1

1.65 x 10⁵ J.

Step-by-step explanation:

We know that the pressure P = 1.55 x 10⁶ N/m² and the radius is r = 0.205 m.

Then, we need to calculate the volume ΔV using the following equation:

`\Delta V=\pi r^2h`

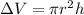
Where h is the distance moved by the piston. So, replacing r = 0.205 m, and h = 0.805 m, we get

`\begin{gathered} \Delta V=\pi(0.205m)^2(0.805\text{ m\rparen} \\ \Delta V=0.106\text{ m}^3 \end{gathered}`

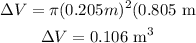
Then, the work done is equal to

`\begin{gathered} W=P\Delta V \\ W=(1.55*10^6\text{ N/m}^2)(0.106\text{ m}^3) \\ W=1.65*10^5\text{ J} \end{gathered}`

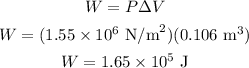
Therefore, the answer is 1.65 x 10⁵ J.