Question

I need help finding the possible coordinates of PI think I got the first part of the question right but I’m struggling on how to get the second part

Answer 1

a.) The Gradient at the point C is 16

b.) Possible coordinate of P is (2, -13)

Step-by-step explanation

Given the equation of the curve C:

`y=x^3-11x+1`

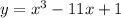
The Gradient at the point on C where x = 3

`\begin{gathered} y=x^3\text{ - 11x + 1} \\ \text{Gradient = }(dy)/(dx)=3x^2\text{ - 11} \\ \text{ }at\text{ x = 3,} \\ \text{Gradient = }(dy)/(dx)=3(3)^2\text{ - 11} \\ \text{Gradient = }(dy)/(dx)=27\text{ - 11} \\ \text{Gradient = }(dy)/(dx)=16 \end{gathered}`

Determine the value of x when the point P lies on C with 1 being the gradient at that point

`\begin{gathered} \text{Gradient = }(dy)/(dx)=3x^2\text{ - 11} \\ \text{1 }=3x^2\text{ - 11} \\ \text{3x}^2\text{ = 1+11} \\ 3x^2\text{ = 12} \\ x^2\text{ = }(12)/(3) \\ x^2\text{ = 4} \\ x\text{ = }\sqrt[]{4} \\ x\text{ = 2} \end{gathered}`

Determine the value of y

`\begin{gathered} y=x^3\text{ - 11x + 1} \\ y=(2)^3\text{ - 11(2) + 1} \\ y\text{ = 8 - 22 + 1} \\ y\text{ = -13} \end{gathered}`

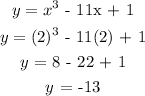
Hence, the possible coordinate of P is (2, -13)