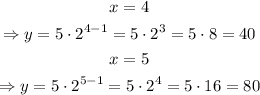Question

when counts by bacteria under microscope she counseling again each day for four days and find the number of bacteria doubled each day from 5 to 10 then 10 to 20 and so on complete the table1. 52.__3.__4. 405.__is the number of bacteria a function of number of days yes or nois it linear yes or no

Answer 1

We have that the first day, there were 5 bacteria, then on day 2 there were 10, and so on. We can write the table like this:

where 'x' represents the number of days and 'y' represents the total bacteria.

Since we are multiplying by 2 each day the total bacteria, we have a geometric sequence, which can be calculated the nth term like this:

`a_n=a_1r^(n-1)`

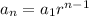
in this case, we can write it like this, considering that the number of bacteria on day 1 is 5, and the common ratio is r = 2 :

`y=5\cdot2^(x-1)`

which clearly is not a linear function, but the number of bacteria is afunction of the number of days.

For the days 4 and 5, we can make x = 4 and x = 5 to get the following:

`\begin{gathered} x=4 \\ \Rightarrow y=5\cdot2^(4-1)=5\cdot2^3=5\cdot8=40 \\ x=5 \\ \Rightarrow y=5\cdot2^(5-1)=5\cdot2^4=5\cdot16=80 \end{gathered}`