Question

Determine the domain and range of the quadratic function. (Enter your answers using interval notation.)f(x) = −8(x + 1)^2 − 8domain= range=

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given Quadratic function

`f(x)=-8(x+1)^2-8`

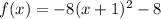
STEP 2: Define the domain and range of a function

We know that the domain of a function is the set of input values for f, in which the function is real and defined. Also, the range of a function comprises the set of values of a dependent variable for which the given function is defined.

STEP 3: Find the domain and the range

Domain: The function has no undefined points nor domain restraints. Therefore, the domain is:

Hence, the answers in interval notation will be given as:

`\begin{gathered} Domain:(-\infty,\infty) \\ Range:(-\infty,-8] \end{gathered}`