The diagram representation is shown below
From the diagram above, it can be seen that the wall, the ground and the ladder form a right-angle triangle
To find the length x of the ladder needed, we use the Pythagorean theorem
The formula for the Pythagorean theorem is
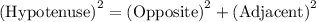
Where
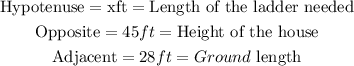
Substitute values into the Pythagorean theorem formula
![\begin{gathered} (\text{Hypotenuse)}^2=(\text{Opposite)}^2+(\text{Adjacent)}^2 \\ x^2=45^2+28^2=2025+784=2809 \\ x^2=2809 \\ \text{Square root of both sides} \\ \sqrt[]{x^2}=\sqrt[]{2809} \\ x=53ft \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/deiwf1fvo31wkilqh9qkniwpu8yj94nnyo.png)
Hence, the ladder must be 53ft long