Question

How many liters each of 10% acid solution and a 80%

Answer 1

Given:

- A 10% acid solution.

- A 80% acid solution.

You need to produce 70 liters of a 65% acid solution.

Let be "t" the number of liters of 10% acid solution that must be used, and "g" the number of liters of 80% acid solution that must be used to produce 70 liters of a 65% acid solution.

By definition, you know that:

`10\text{ \%}=(10)/(100)=0.1`
`80\text{ \%}=(80)/(100)=0.8`
`65\text{ \%}=(65)/(100)=0.65`

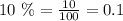
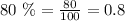
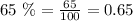
Therefore, you can set up the following System of Equations using the data provided in the exercise:

`\begin{cases}0.1t+0.8g=0.65(70){} \\ t+g=70{}\end{cases}`

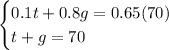
Use the Substitution Method to solve it:

1. Solve the second equation for "t":

`t=70-g`

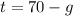
2. Substitute it into the first equation and solve for "g":

`0.1(70-g)+0.8g=45.5`
`\begin{gathered} 7-0.1g+0.8g=45.5 \\ 0.7g=45.5-7 \\ \\ g=(38.5)/(0.7) \\ \\ g=55 \end{gathered}`

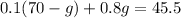
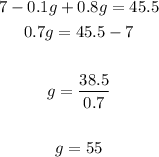
3. Substitute the value of "g" into this equation and then evaluate:

`t=70-g`

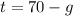
Then:

`\begin{gathered} t=70-55 \\ t=15 \end{gathered}`

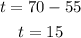
Hence, the answer is:

• 15 liters of 10% acid solution.

,

• 55 liters of 80% acid solution.