The diagonal of a rectangle forms a right triangle with the sides. This means that we can apply Pythagora's theorem to calculate the length of the diagonal. This is done below:
![\begin{gathered} AC^2=3^2+12^2 \\ AC^2=9+144 \\ AC^2=153 \\ AC=\sqrt[]{153=\sqrt[]{9\cdot17}} \\ AC=3\cdot\sqrt[]{17} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/m7mh3o9ps6a5nl4l4wprq6qur2votqmhql.png)
The answer is 3sqrt(17).
To find the angles we need to apply the trigonometric relationships on the right triangle. They can be both found by using the tangent. This is done below:

To find the values of the angles we need to apply the inverse of the tangent to them. We have:
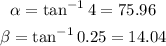
The angles are alpha = 75.96° and beta = 14.04°