Question

A resort in Orlando, Florida offers vacationers two boat ride plans. Plan A gives 3 nights lodging and 5 boat rides for a total cost of $625. Plan B gives 5 nights lodging and 6 boat rides for a total of $960What is the cost of each boat ride?

Answer 1

Given is Plan A gives 3 nights lodging and 5 boat rides for a total cost of $625.

and Plan B gives 5 nights lodging and 6 boat rides for a total of $960.

Let x be the cost of night lodging and y be the cost of the boat ride.

The given can be written as follows.

`3x+5y=625`
`5x+6y=960`

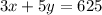
Multiply equation 3x+5y=625 by 5 as follows.

`5*3x+5*5y=5*625`

`15x+25y=3125\text{ take it as equation (1).}`

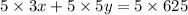
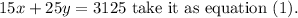
Multiply equation 5x+6y=960 by 3 as follows.

`3*5x+3*6y=3*960`

`15x+18y=2880\text{ take this as equation (2).}`

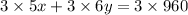
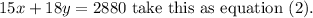
Substract equation (2) from equation (1) to compute the value of y.

`(15x+25y)-(15x+18y)=3125-2880`

`15x+25y-15x-18y=3125-2880`

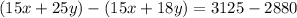
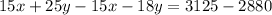
Solve like terms.

`7y=245`

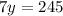
Dividing by 7 into both sides, we get

`(7y)/(7)=(245)/(7)`

`y=35`

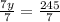
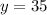
Hence we get the cost of the boat ride is $35.

Substitute y=35 in 3x+5y=625 to compute the value of y.

`3x+5(35)=625`

`3x+175=625`

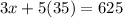
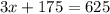
Adding -175 on both sides, we get

`3x+175-175=625-175`

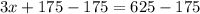
Solve like terms.

`3x=450`

Dividing by 3 into both sides, we get

`(3x)/(3)=(450)/(3)`

`x=150`

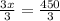
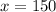
Hence the cost of night lodging is $150.

Result :

The cost of night lodging is $150.

The cost of the boat ride is $35.

The cost of each boat is $150 and $35.