We have the system
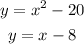
So we can equalize the two equations to get x
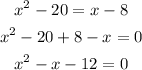
So now we can solve the quadratic equation to find x, we are going to use the quadratic formula
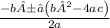
We have a = 1, b= - 1 and c = -12, so replacing we get
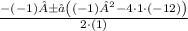
this is

Then the solutions for x are x = (1 - 7)/2 = -6/2 = -3, and x = (1+7)/2 = 8/2 = 4. Now we replace in the second equation and we get two solutions for y, using x = -3 we get y = -3 - 8 = -11, and using x = 4 we get y = 4 - 8 = -4. So the two points are: (-3,-11) and (4,-4). THE ANSWER IS D.