Question

The functions s and t are defined as follows.s(x) = 2x + 2t(x)=-2x²-2Find the value of t(s(-4)).

Answer 1

As per given by the solution,

There are given that the equation,

`\begin{gathered} s(x)=2x+2 \\ t(x)=-2x^2-2 \end{gathered}`

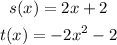
Now,

According to the question, find the value of t(s(-4)).

Then,

First find the value of s(-4);

So,

The given equation is ,

`s(x)=2x+2`

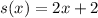
Put the value of x =-4 into above equation,

Then,

`\begin{gathered} s(x)=2x+2 \\ s(-4)=2*(-4)_{}+2 \\ s(-4)=-8+2 \\ s(-4)=-6 \end{gathered}`

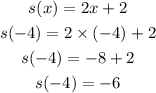
Now,

For finding the value of t(s(-4)):

From the second equation,

`t(x)=-2x^2-2`

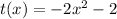
In above equation, put the value of s(-4) instead of x.

So,

`\begin{gathered} t(x)=-2x^2-2 \\ t(s(-4))=-2*(-6)^2^{}-2 \\ t(s(-4))=-2*36-2 \\ t(s(-4))=-72-2 \\ t(s(-4))=-74 \end{gathered}`

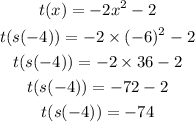
Hence, the value of t(s(-4)) is -74.