Step 1:
First, find the total number of students.
Let the total number of students = m
Step 2:
Find the total number of students using the percentage of 4 books.
48 students listed 4 books with a percentage of 16%
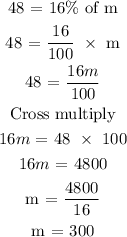
Hence, there are 300 students.
a)
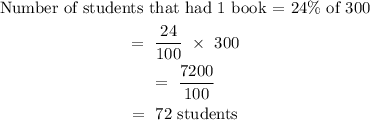
72 students had 1 book.
b) What percentage more read 2 books than 4 books?
percentage that read 2 books = 36%
percentage that read 4 books = 16%
36 - 16 = 20%
There are 20% students that read 2 books than 4 books.