Question

In ΔABC, Z is the midpoint of AC and Y is the midpoint of BC. If YZ = 21 and AB = (2x – 4), what is the value of x?

Answer 1

C. 23

Step-by-step explanation

We are given that Z is the midpoint of AC and Y is the midpoint of BC.

According to the midpoint theorem of triangles, the midsegment of a triangle (YZ) is equal to half the length of side parallel to it (AB)

This means that:

`YZ\text{ = }(1)/(2)AB`

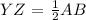
So, we have that:

`\begin{gathered} 21\text{ = }(1)/(2)(2x\text{ - 4)} \\ 21\text{ = x - 2} \\ \text{Collect like terms:} \\ \Rightarrow\text{ x = 21 + 2} \\ \text{x = 23} \end{gathered}`

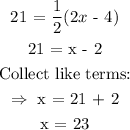
The answer is Option C.