Question

Find the length of BE Show exact steps to solve

Answer 1

Given the line segment BE

As shown:

BC = 3x + 47

CD = y

BD = x + 27

CE = x + 26

DE = 10

To find the length of BE, we will find the values of x and y

So,

`\begin{gathered} y=BD-BC \\ y=(x+27)-(3x+47) \\ y=-2x-20\rightarrow(1) \\ y=x+26-10 \\ y=x+16\rightarrow(2) \end{gathered}`

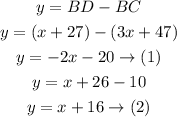
Solve the equations (1) and (2) for x

`\begin{gathered} x+16=-2x-20 \\ x+2x=-20-16 \\ 3x=-36 \\ x=-(36)/(3)=-12 \end{gathered}`

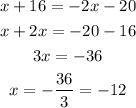
Substitute at (2) to find y

`y=x+16=-12+16=4`

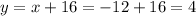
The length of BE = BC + CD + DE

`BE=(3x+47)+y+10`

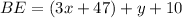
Substitute with x and y:

`\begin{gathered} BE=3\cdot-12+47+4+10 \\ BE=25 \end{gathered}`

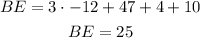
So, the answer will be ⇒ BE = 25